Gfyuki

Rekto estas speciala speco de kurbo. En ĉiutaga lingvo signifas ne kurba, sen larĝa. Ĉi tiu priskribo bone priskribas rekton en kartezia koordinato. Sed en matematiko estas ankaŭ aliaj koordinatoj. Tiam rekto nomiĝas geodezia linio.

Difino |

Rekto estas aro de punktoj tiaj, ke distanco inter laŭvolaj du punktoj estas plej mallonga.

Rekto en 2D kartezia spaco |

Universala ekvacio de rekto |

Universala ekvacio de rekto estas formulo:

A x + B y + C = 0

kie A, B, C - laŭvolaj reelaj nombroj .Sed almenaŭ unu el A kaj B ne estas nulo.

(x, y) - koordinatoj de punkto en rekto.

Vektoro [A, B] estas orta al rekto, kaj vektoro [-A, B] estas paralela al rekto.

Rimarku: unu rekto povas havi pli ol unu universala ekvacio. Sed koeficiento devas: A1A2=B1B2=C1C2{displaystyle {frac {A_{1}}{A_{2}}}={frac {B_{1}}{B_{2}}}={frac {C_{1}}{C_{2}}}}. Ĉar oni sufiĉas ke universala ekvacio multiplikas de laŭvola ne nula nombro kaj oni estos alia ekvacio sed ĝi priskribos saman rekton.

Norma ekvacio de rekto |

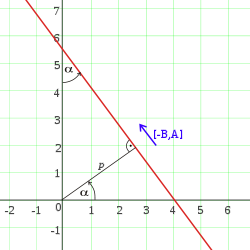
Ĉar mulataj universalaj ekvacioj povas priskribi unu rekto, tial oni estas ebleco por ke normi trans oni dividas koeficientoj A{displaystyle A}, B{displaystyle B} i C{displaystyle C} per longeco de normo de direkta vektoro:

{A′=AμB′=BμC′=Cμ{displaystyle {begin{cases}A'=Amu \B'=Bmu \C'=Cmu end{cases}}},

kaj μ{displaystyle mu } estas normanta frakto:

μ=1A2+B2{displaystyle mu ={frac {1}{sqrt {A^{2}+B^{2}}}}} por C<0{displaystyle C<0} aŭ μ=−1A2+B2{displaystyle mu ={frac {-1}{sqrt {A^{2}+B^{2}}}}} por C>0{displaystyle C>0}

por C=0{displaystyle C=0} oni eblas doni laŭvolan signon al μ{displaystyle mu }.

Koeficientoj de ĉi tiu ekvacio estas de speciala signifo, ĉar oni skribas ankaŭ kiel:

xcos⁡α+ysin⁡α−p=0{displaystyle xcos alpha +ysin alpha -p=0,},

ĉi tiu estas normala ekvacio de rekto kaj α{displaystyle alpha } estas angulo inter rekto kaj Oy{displaystyle Oy} kaj p{displaystyle p} estas distanco inter centro de sistemo de koordinatoj kaj rekto. Kaj 0≤α<2π{displaystyle 0leq alpha <2pi }.

Direkta ekvacio |

Rektoj kun ekvacioj

Direkta ekvacio de rekto estas formulo:

y=ax+b{displaystyle y=ax+b,}

kaj a, b estas reelaj nombroj.

• 
  a estas direkta faktoro de rekto. Ĉiuj du rektoj kun sama direkta faktoro estas paralela. Kaj estas ekvivalento al tangento de angulo inter rekto kaj Ox. a=−AB{displaystyle a=-{frac {A}{B}}}
  


• 
  b estas libera faktoro. Valoro de libera faktoro estas punkto en kiu rekto kruciĝas kun Oy.

Parametra ekvacio |

Parametra difino de rekto. Ĉi tie
x_B=x_A+u₁, y_B=y_A+u₂
Vidu tekston por priskribo de la valoroj.

Rekto l kun nenula direkta vektoro α=[u1,u2]{displaystyle alpha =[u_{1},u_{2}]}, kaj trakuras tra punkto A=(xA,yA){displaystyle A=(x_{A},y_{A})} estas aro de punktoj P=(x,y){displaystyle P=(x,y)}:

P=A+tα{displaystyle P=A+talpha } por ĉiuj t∈R{displaystyle tin mathbb {R} }.

Alinome:

l={A+tα:t∈R}{displaystyle l={A+talpha colon tin mathbb {R} }}

aŭ:

l=A+lin(α){displaystyle l=A+{mbox{lin}}(alpha )}.

Koeficienta sistemo de ekvacioj:

{x=xA+tu1y=yA+tu2{displaystyle left{{begin{matrix}x=x_{A}+tu_{1}\y=y_{A}+tu_{2}end{matrix}}right.}

xA{displaystyle x_{A}} kaj yA{displaystyle y_{A}} estas laŭvolaj reelaj nombroj, sed u1{displaystyle u_{1}} kaj u2{displaystyle u_{2}} ne povas esti nulo samtempe tiam sistemo estos priskribi nur unu punkton ne ĉiun rekton.

Vidu ankaŭ |

• Kurbo


• Ebeno


• Rekta streko


• Duonrekto

Eksteraj ligiloj |

• 
  Rekta linio je MathWorld


• 
  Ekvacioj de rekta linio je tranĉi-la-nodon