Gfyuki

Dekduedro, unu el la kvin 3-dimensiaj konveksaj regulaj hiperpluredroj - platonaj solidoj.

En matematiko, regula hiperpluredro estas hiperpluredro kun alta grado de simetrio. Ĝi estas pli alta-dimensia analoga de regulaj plurlateroj (ekzemple, la kvadrato aŭ la regula kvinlatero) kaj regulaj pluredroj (ekzemple, la kubo). Cirkloj kaj sferoj, kvankam alte simetriaj, ne estas konsiderataj kiel hiperpluredroj ĉar ili ne havas ebenajn edroj.

Regula hiperpluredro havas jenajn propraĵojn:

• Ĝi estas simetria tiel ke ĝiaj hiperĉeloj de ĉiu dimensio de 0 ĝis n-1 estas egalaj, kaj se koincidigi la hiperĉelon ankaŭ la tuta hiperpluredro povas esti koincidigita. Do, ĝi estas
  
  
  
  • 
    vertico-transitiva,
  
  
  • 
    latero-transitiva,
  
  
  • 
    edro-transitiva,
  
  
  • 
    ĉelo-transitiva,
  
  
  • 4-hiperĉelo-transitiva,
  
  
  • 5-hiperĉelo-transitiva,
  
  
  • ... ,
  
  
  • 
    kulmino-transitiva,
  
  
  • 
    kresto-transitiva,
  
  
  • 
    faceto-transitiva.
  
  
  
  


• Ĝiaj hiperĉeloj de ĉiu dimensio de 2 ĝis n-1 estas mem regulaj hiperpluredroj (0-dimensiaj kaj 1-dimensiaj hiperpluredroj ĉiam estas regulaj). Do, ĝiaj
  
  
  
  • 
    edroj estas regulaj plurlateroj,
  
  
  • 
    ĉeloj estas regulaj pluredroj,
  
  
  • 4-hiperĉeloj estas regulaj plurĉeloj,
  
  
  • 5-hiperĉeloj estas regulaj 5-hiperpluredroj,
  
  
  • ... ,
  
  
  • 
    kulminoj estas regulaj n-3-hiperpluredroj,
  
  
  • 
    krestoj estas regulaj n-2-hiperpluredroj,
  
  
  • 
    facetoj estas regulaj n-1-hiperpluredroj.
  
  
  
  

Difino |

La difino de regula hiperpluredro estas la sekva:

• Plurlatero estas regula se ĝiaj lateroj estas ĉiuj egalaj kaj kies anguloj estas ĉiuj egalaj.


• 
  n-hiperpluredro estas regula se ĝiaj (n-1)-dimensiaj facetoj estas ĉiuj regulaj kaj kongruaj, kaj ĝiaj verticaj figuroj estas ĉiuj regulaj kaj kongruaj.

Ĉi tiu estas rekursia difino. Ĝi difinas regulecon de figuroj de iu dimensioper reguleco de figuroj de la suba dimensio. ekzemple, por n=3, la dua propozicio de la difino aspektas kiel:

Pluredro estas regula se ĝiaj edroj estas ĉiuj kongruaj regulaj plurlateroj, kaj ĝiaj verticaj figuroj estas ĉiuj kongruaj kaj regulaj.

Estas ekvivalenta ne rekursia difino, kiuj donas ke hiperpluredro estas regula se ĝi havas sufiĉan gradon de simetrio:

• 
  n-hiperpluredro estas regula se ĉiu aro konsistanta el vertico, latero enhavanta la verticon, edro enhavanta la lateron, kaj tiel plu ĝis al n-1 dimensioj, povas esti mapita al ĉiu la alia ĉi tia subaro de la hiperpluredro per simetrio de la hiperpluredro.

Do, ekzemple, kubo estas regula ĉar se oni elektas verticon de la kubo, unuon el la tri lateroj enhavantaj la verticon, kaj unuon el la du edroj enhavantaj la lateron, tiam ĉi tiu trio, aŭ flago, povas esti mapita al ĉiu la alia tia flago per taŭga simetrio de la kubo.

Klasifiko |

Regulaj hiperpluredroj estas klasifikitaj unuavice laŭ iliaj kvantoj de dimensioj.

Ili povas esti plu klasifikitaj laŭ simetrio. Ekzemple la kubo kaj la regula okedro (komunigi, parto) la sama simetrio, kiel fari la regula dekduedro kaj dudekedro. Ja, geometriaj simetriaj grupoj estas iam nomis post regulaj hiperpluredroj, ekzemple la kvaredra kaj dudekedraj simetrioj.

Tri specialaj klasoj de regulaj hiperpluredroj ekzistas en ĉiu dimensinombro:

• Regula simplaĵo
  


• Hiperkubo


• Kruco-hiperpluredro

En du dimensioj estas malfinie multaj regulaj plurlateroj. En tri kaj kvar dimensioj estas kelkaj pliaj regulaj pluredroj kaj regulaj plurĉeloj ekster ĉi tiuj tri. En kvin dimensioj kaj pli supre, ĉi tiuj tri estas la solaj aĵoj.

Regulaj hiperpluredroj estas ankaŭ disdividitaj je konveksaj kaj nekonveksaj.

Vidu en la listo de regulaj hiperpluredroj.

Simbolo de Schläfli |

Pli detalaj informoj troveblas en la artikolo Simbolo de Schläfli.

Simbolo de Schläfli estas skribmaniero de regulaj pluredroj. La skribmaniero estas plej bona eksplikita per aldonado po unu dimensio.

• 2-dimensia konveksa regula plurlatero havanta n laterojn estas skribata kiel {p}. Do egallatera triangulo estas {3}, kvadrato {4}, kaj tiel plu. Regula stelo kiu kirliĝas m fojojn ĉirkaŭ sia centro estas skribata kiel la frakcia valoro {p/m}, kie p kaj m estas kunprimoj, do regula stelokvinlatero estas {5/2}.

• 3-dimensia regula pluredro havantaj edrojn ĉiu de speco {p} kun q edroj ĉirkaŭ vertico estas skribata kiel {p, q}. La naŭ regulaj pluredroj estas {3, 3} {3, 4} {4, 3} {3, 5} {5, 3} {5, 5/2} {5/2, 5} {3, 5/2}, {5/2, 3}. {q} estas la vertica figuro de la pluredro.

• 4-dimensia regula plurĉelo havantaj ĉelojn ĉiu de speco {p, q} kun r ĉeloj ĉirkaŭ vertico estas skribata kiel {p, q, r}. La vertica figuro de la plurĉelo estas {q, r}.

• 5-dimensia regula hiperpluredro estas {p, q, r, s}, kaj tiel plu.

Dualeco de la regulaj hiperpluredroj |

Ankaŭ la duala hiperpluredro de regula hiperpluredro estas regula hiperpluredro. La Simbolo de Schläfli de la duala hiperpluredro estas la originala simbolo skribita malantaŭen: {3, 3} estas mem-duala, {3, 4} estas duala al {4, 3}, {4, 3, 3} al {3, 3, 4} kaj tiel plu.

La vertica figuro de regula hiperpluredro estas duala al faceto de la duala hiperpluredro kaj ree. Ekzemple la vertica figuro de {3, 3, 4} estas {3, 4}, kiu estas duala al {4, 3} kiu estas faceto (ĉelo) de {4, 3, 3}.

Ĉiu regula plurlatero estas mem-duala.

Regula simplaĵo estas mem-duala, dum la mezuri kaj kruci hiperpluredroj estas duala al unu la alian.

Ĝeneraligoj |

La ideo de hiperpluredro estas iam ĝeneraligis al inkluzivi (rilatanta, parenca, rilata) (afablaj, specoj) de geometria objekto. Iu de ĉi tiuj havi regulaj ekzemploj, kiel diskutis en la sekcio sur historia malkovro pli sube.

Malfiniaj regulaj hiperpluredroj |

Malfiniaj regulaj hiperpluredroj aŭ regulaj malfinioedroj estas ekzemple {4, 6}, {6, 4} kaj {6, 6}. Ili kontentigas la difinon de regula pluredro - ĉiuj verticoj, lateroj kaj edroj estas egalaj, ĉiuj anguloj estas la samaj, kaj la figuro havas ne liberajn lateroj (ĉar ili povas neniam esti atingita). Ankaŭ regulaj kahelaroj de eŭklida ebeno {4, 4} {3, 6} kaj {6, 3} povas esti konsiderataj kiel malfiniaj pluredroj.

Malfiniolatero estas plurlatero kun malfinie multaj lateroj. Regulaj hiperpluredroj kun malfinie multaj edroj. Simpla ekzemplo de malfiniolatero {∞} havas zigzagan formon. Ĝi kontentigas la difinon de regula plurlatero - ĉiuj lateroj estas de la sama longo, ĉiuj anguloj estas la samaj, kaj la figuro ne havas finojn (ĉar ili povas neniam esti atingitaj). Pli grave, estas simetrioj de la zigzago kiuj mapas ĉiun paron de vertico kaj alfiksita latero al ĉiu la alia.

Kompleksaj regulaj hiperpluredroj |

Hermita spaco havas siajn koordinatojn kiel kompleksaj nombroj. Ĉi tio efike duobligas kvanton de la dimensioj, ĉar ĉiu kompleksa koordinato havas reelan parton kaj imaginaran parton, ĉiu el kiuj estas sendependa reela nombro.

Hiperpluredro konstruita en hermita spaco estas kompleksa hiperpluredro.

Abstraktaj regulaj hiperpluredroj |

Pli detalaj informoj troveblas en la artikolo Abstrakta hiperpluredro.

Duonkubo

Abstrakta regula hiperpluredro estas difinita kiel aro, supozita al prezenti la aron de verticoj, lateroj, edroj kaj tiel plu de hiperpluredro, kun ideo rilate al tio kiuj el ĉi tiuj koincidas kiu la aliaj. Certaj limigoj estas aldonitaj, la limigoj estas similaj al propraĵoj kontentigita per la klasikaj regulaj hiperpluredroj.

La duonkubo estas konstruita el kubo per konsiderado de la kontraŭaj lateroj (kaj ankaŭ edroj kaj anguloj) kiel reale la samaj. Ĝi havas 3 edroj, 6 laterojn, kaj 4 verticojn.

La 3-dimensiaj abstraktaj regulaj pluredroj estas ankaŭ duon-dudekedro kaj duon-dekduedro.

La 4-dimensiaj abstraktaj regulaj plurĉeloj estas ankaŭ 11-ĉelo kaj 57-ĉelo.

Geometria hiperpluredro estas kompreno de la abstrakta hiperpluredro, se ĝi ekzistas bijekcio de la abstraktaj eroj al la geometriaj. Tial, ĉiu geometria hiperpluredro povas esti priskribita per la konvena abstrakta parte ordita aro, kvankam ne ĉiuj abstraktaj hiperpluredroj havi pozitivajn geometriajn komprenojn.

Konstruoj |

Normale, por abstraktaj regulaj hiperpluredroj, oni konsideras ke la objekto estas "konstruita" se la strukturo de ĝia geometria simetria grupo estas sciata.
Tamen eblas provi konstrui pli fizikan modelon.

Plurlateroj |

Ĉiu regula plurlatero povas esti desegnita sur ebeno.

Tamen, la klasika vojo por konstrui regulan plurlateron sur la ebeno estas per cirkelo kaj liniilo. Iuj regulaj plurlateroj tiamaniere estas konstrueblaj iuj simple, iuj malpli simple, kaj iuj estas nekonstrueblaj. La unuaj regulaj plurlateroj kiujn neeblas konstrui estas tuj kun 7, 9, 11, 13, 14, 18, 19, 21, 22, ... lateroj. Konstruebleco en ĉi tiu senco temas nur pri idealaj konstruoj per idealaj iloj. Proksimumaj konstruoj povas esti eblaj praktike kaj teorie eblaj konstruoj povas esti nepraktikaj.

Pluredroj |

[[Dosiero:Cuboctahedron flat.svg|thumb|[[Reto de kubokedro]]
La plej komuna vojo prezenti konstruon de regula pluredro estas per ĝia reto (malfaldaĵo) (reto, neta, reta hiperpluredro)]]. Se ĉi tiu reto estas desegnita sur kartono, lado aŭ la alia faldebla, la reto povas esti eltranĉi, faldita laŭ la krudaj randoj, kunigita laŭ la konvena tranĉitaj lateroj, kaj do formiĝas rando de la pluredro. Por donita pluredro povas esti multaj malfaldaĵoj. Ekzemple, ili estas 11 por kubo, kaj pli ol 900000 por dekduedro.

Multaj porinfanaj ludiloj permesi konstrui regulajn plurlaterojn kaj pluredrojn. Origamio povas uzata.

Pli altaj dimensioj |

Reto de senpintigita 4-hiperkubo

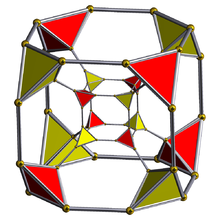
Perspektiva projekcio (figuro de Schlegel) por senpintigita 4-hiperkubo kun kvaredraj ĉeloj videblaj

En 3-dimensia universo, neeblas konstrui fizikan modelon de objekto havanta 4 aŭ pli dimensiojn. Estas kelkaj manieroj tamen fari la aferon:

• Konstrui reton, kiu estas je 1 malpli dimensia.


• 
  Projekcii la objekton en 3-spacon. Ekzemple, komunaĵo de kvar aŭ pli alte dimensia regula hiperpluredro kun tri-dimensia hiperebeno estas pluredro (ne nepre regula). Se la hiperebeno estas movata tra la formo, la tri-dimensiaj tranĉaĵoj ŝanĝiĝas, farante animacion.


• 4-dimensia plurĉelo povas esti konsiderata kahelaro de 3-dimensia ne-eŭklida spaco, nome, kahelaro de la surfaco de 3-sfero. Virtuala realeco povas meti vidanton en ĉi tiun spacon. Por kompreni kiel ĉi tiu povus laboro, imagu kion oni devus vidi se spaco plenigita de kuboj (kuba kahelaro). La vidanto devus esti en unu el la kuboj, kaj devus kapabli vidi kubojn antaŭ, malantaŭ, pli supre, pli sube, maldekstre kaj dekstre de si. Se unu povita vojaĝi en ĉi tiuj direktoj, onu povita esplori la tabelo de kuboj, kaj kompreni ĝian geometrian strukturon. La kuba kahelaro tamen estas kahelaro de 3-dimensia eŭklida spaco.

Vidu ankaŭ |

• Listo de regulaj hiperpluredroj


• Simbolo de Schläfli


• Uniforma hiperpluredro


• Solido de Johnson


• Grupo de Coxeter

Eksteraj ligiloj |

• 
  George Olshevsky, Regula hiperpluredro en Glossary for Hyperspace.


• 
  [1] de Ernst Haeckel


• Retoj de kubo, okedro, dekduedro kaj dudekedro