Gfyuki

Ĉi tiu tabelo enhavas indeksitan liston de la uniformaj kaj steligitaj pluredroj de la libro Pluredraj Modeloj de Magnus Wenninger.

La libro estis skribita kiel gvidilo por konstrui pluredrojn kiel fizikaj modeloj. Ĝi inkluzivas ŝablonojn de la edroj por konstruado, kaj ankaŭ mallonge priskribas la teorion malantaŭ de ĉi tiuj formoj.

Ĝi enhavas la 75 neprismajn uniformajn pluredrojn, kaj ankaŭ 44 steligitajn formojn de konveksaj regulaj pluredroj.

Specoj de pluredroj listigitaj ĉi tie povas esti referencitaj kiel "Modelo de Wenninger numero N", aŭ W_N.

La pluredroj estas grupitaj pli sube en 5 tabelojn: regula (1 ... 5), duonregula (6 ... 18), regulaj stelaj pluredroj (20 ... 22, 41), steligoj kaj kombinaĵoj (19 ... 66), kaj uniformaj stelaj pluredroj (67 ... 119). La kvar regulaj stelaj pluredroj estas listitaj dufoje ĉar ili apartenan kaj al uniformaj pluredroj kaj al stelaj.

Platonaj solidoj (regulaj) W1 ... W5 |

Indekso	Nomo	Bildo	Simbolo de Wythoff	Vertica figuro kaj simbolo de Schläfli	Geometria simetria grupo	U#	K#	V	E	F	Edroj laŭ speco
1	Kvaredro		3|2 3	{3,3}	Td	U01	K06	4	6	4	4{3}
2	Okedro		4|2 3	{3,4}	Oh	U05	K10	6	12	8	8{3}
3	Kubo		3|2 4	{4,3}	Oh	U06	K11	8	12	6	6{4}
4	Dudekedro		5|2 3	{3,5}	Ih	U22	K27	12	30	20	20{3}
5	Dekduedro		3|2 5	{5,3}	Ih	U23	K28	20	30	12	12{5}

Arĥimedaj solidoj (duonregulaj) W6 ... W18 |

Indekso	Nomo	Bildo	Simbolo de Wythoff	Vertica figuro	Geometria simetria grupo	U#	K#	V	E	F	Edroj laŭ speco
6	Senpintigita kvaredro		2 3|3	3.6.6	Td	U02	K07	12	18	8	4{3}+4{6}
7	Senpintigita okedro		2 4|3	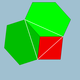4.6.6	Oh	U08	K13	24	36	14	6{4}+8{6}
8	Senpintigita sesedro		2 3|4	3.8.8	Oh	U09	K14	24	36	14	8{3}+6{8}
9	Senpintigita dudekedro		2 5|3	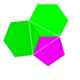5.6.6	Ih	U25	K30	60	90	32	12{5}+20{6}
10	Senpintigita dekduedro		2 3|5	3.10.10	Ih	U26	K31	60	90	32	20{3}+12{10}
11	Kubokedro		2|3 4	3.4.3.4	Oh	U07	K12	12	24	14	8{3}+6{4}
12	Dudek-dekduedro		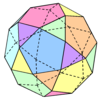2|3 5	3.5.3.5	Ih	U24	K29	30	60	32	20{3}+12{5}
13	Malgranda rombokub-okedro		3 4|2	3.4.4.4	Oh	U10	K15	24	48	26	8{3}+(6+12){4}
14	Malgranda rombo-dudek-dekduedro		3 5|2	3.4.5.4	Ih	U27	K32	60	120	62	20{3}+30{4}+12{5}
15	Granda rombokub-okedro (Rombotranĉita kubokedro) (Senpintigita kubokedro)		2 3 4|	4.6.8	Oh	U11	K16	48	72	26	12{4}+8{6}+6{8}
16	Granda rombo-dudek-dekduedro (Rombotranĉita dudek-dekduedro) (Senpintigita dudek-dekduedro)		2 3 5|	4.6.10	Ih	U28	K33	120	180	62	30{4}+20{6}+12{10}
17	Riproĉa kubo		|2 3 4	3.3.3.3.4	O	U12	K17	24	60	38	(8+24){3}+6{4}
18	Riproĉa dekduedro		|2 3 5	3.3.3.3.5	I	U29	K34	60	150	92	(20+60){3}+12{5}

Solidoj de Keplero-Poinsot (regulaj stelaj pluredroj) W20, W21, W22, W41 |

Indekso	Nomo	Bildo	Simbolo de Wythoff	Vertica figuro kaj simbolo de Schläfli	Geometria simetria grupo	U#	K#	V	E	F	Edroj laŭ speco
20	Malgranda steligita dekduedro		5|25/2	{5/2,5}	Ih	U34	K39	12	30	12	12{5/2}
21	Granda dekduedro		5/2|2 5	{5,5/2}	Ih	U35	K40	12	30	12	12{5}
22	Granda steligita dekduedro		3|25/2	{5/2,3}	Ih	U52	K57	20	30	12	12{5/2}
41	Granda dudekedro (16-a steligo de dudekedro)		5/2|2 3	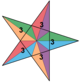{3,5/2}	Ih	U53	K58	12	30	20	20{3}

Steligoj W19 ... W66 |

Steligo de okedro |

Indekso	Nomo	Geometria simetria grupo	Bildo	Facetoj
2	Okedro (regula)	Oh
19	Steligita okedro (Kombinaĵo de du kvaredroj)	Oh

Steligoj de dekduedro |

Indekso	Nomo	Geometria simetria grupo	Bildo	Facetoj
5	Dekduedro (regula)	Ih
20	Malgranda steligita dekduedro (regula) (Unua steligo de dekduedro)	Ih
21	Granda dekduedro (regula) (Dua steligo de dekduedro)	Ih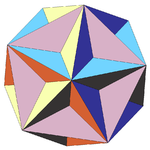
22	Granda steligita dekduedro (regula) (Tria steligo de dekduedro)	Ih

Steligoj de dudekedro |

Indekso	Nomo	Geometria simetria grupo	Bildo	Facetoj
4	Dudekedro (regula)	Ih
26	Unua steligo de dudekedro (Trilateropiramidigita dudekedro)	Ih
23	Kombinaĵo de kvin okedroj (Unua kombinaĵa steligo de dudekedro)	Ih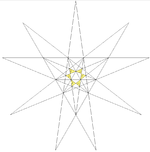
24	Kombinaĵo de kvin kvaredroj (Dua kombinaĵa steligo de dudekedro)	I
25	Kombinaĵo de dek kvaredroj (Tria kombinaĵa steligo de dudekedro)	Ih
27	Dua steligo de dudekedro	Ih
28	Tria steligo de dudekedro	Ih
29	Kvara steligo de dudekedro	Ih
30	Kvina steligo de dudekedro	Ih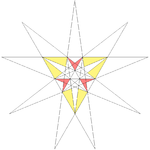
31	Sesa steligo de dudekedro	Ih
32	Sepa steligo de dudekedro	Ih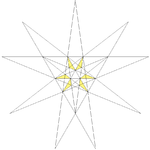
33	Oka steligo de dudekedro	Ih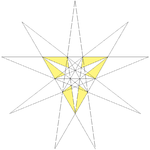
34	Naŭa steligo de dudekedro	Ih
35	Deka steligo de dudekedro	I
36	Dekunua steligo de dudekedro	I
37	Dekdua steligo de dudekedro	Ih
38	Dektria steligo de dudekedro	I
39	Dekkvara steligo de dudekedro	I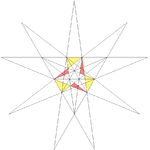
40	Dekkvina steligo de dudekedro	I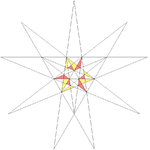
41	Granda dudekedro (regula) (Deksesa steligo de dudekedro)	Ih
42	Fina steligo de la dudekedro	Ih

Steligoj de kubokedro |

Indekso	Nomo	Geometria simetria grupo	Bildo	Facetoj de okedraj ebenoj	Facetoj de kubaj ebenoj
11	Kubokedro (regula)	Oh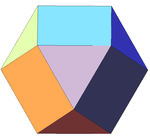
43	Kombinaĵo de kubo kaj okedro (Unua steligo de kubokedro)	Oh
44	Dua steligo de kubokedro	Oh
45	Tria steligo de kubokedro	Oh
46	Kvara steligo de kubokedro	Oh

Steligoj de dudek-dekduedro |

Indekso	Nomo	Geometria simetria grupo	Bildo	Facetoj de dudekedraj ebenoj	Facetoj de dekduedraj ebenoj
12	Dudek-dekduedro (regula)	Ih
47	(Unua steligo de dudek-dekduedro) Kombinaĵo de dekduedro kaj dudekedro	Ih
48	Dua steligo de dudek-dekduedro	Ih
49	Tria steligo de dudek-dekduedro	Ih
50	Kvara steligo de dudek-dekduedro (Kombinaĵo de malgranda steligita dekduedro kaj trilateropiramidigita dudekedro)	Ih
51	Kvina steligo de dudek-dekduedro (Kombinaĵo de malgranda steligita dekduedro kaj kvin okedroj)	Ih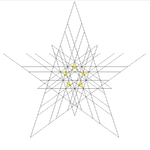
52	Sesa steligo de dudek-dekduedro	Ih
53	Sepa steligo de dudek-dekduedro	Ih
54	Oka steligo de dudek-dekduedro (Kombinaĵo de kvin kvaredroj kaj granda dekduedro)	I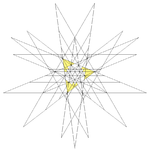
55	Naŭa steligo de dudek-dekduedro	Ih
56	Deka steligo de dudek-dekduedro	Ih
57	Dek-unua steligo de dudek-dekduedro	Ih
58	Dek-dua steligo de dudek-dekduedro	Ih
59	Dek-tria steligo de dudek-dekduedro	Ih
60	Dek-kvara steligo de dudek-dekduedro	Ih
61	Kombinaĵo de granda steligita dekduedro kaj granda dudekedro	Ih
62	Dek-kvina steligo de dudek-dekduedro	Ih
63	Dek-sesa steligo de dudek-dekduedro	Ih
64	Dek-sepa steligo de dudek-dekduedro	Ih
65	Dek-oka steligo de dudek-dekduedro	Ih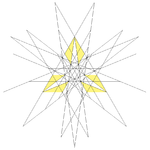
66	Dek-naŭa steligo de dudek-dekduedro	Ih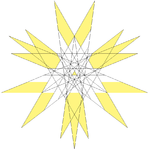

Uniformaj nekonveksaj solidoj W67 ... W119 |

Indekso	Nomo	Bildo	Simbolo de Wythoff	Vertica figuro	Geometria simetria grupo	U#	K#	Verticoj	Lateroj	Edroj	Edroj laŭ speco
67	Kvar-duon-sesedro		3/23|2	4.3/2.4.3	Td	U04	K09	6	12	7	4{3}+3{4}
68	Ok-duon-okedro		3/23|3	6.3/2.6.3	Oh	U03	K08	12	24	12	8{3}+4{6}
69	Malgranda kubokubo-okedro		3/24|4	8.3/2.8.4	Oh	U13	K18	24	48	20	8{3}+6{4}+6{8}
70	Malgranda du-tritranĉa dudek-dekduedro		3|5/23	(5/2.3)3	Ih	U30	K35	20	60	32	20{3}+12{5/2}
71	Malgranda dudek-dudek-dekduedro		5/23|3	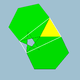6.5/2.6.3	Ih	U31	K36	60	120	52	20{3}+12{5/2}+20{6}
72	Malgranda dekdu-dudek-dekduedro		3/25|5	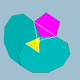10.3/2.10.5	Ih	U33	K38	60	120	44	20{3}+12{5}+12{10}
73	Dekduedro		2|5/25	(5/2.5)2	Ih	U36	K41	30	60	24	12{5}+12{5/2}
74	Malgranda rombo-dekduedro		25/25|	10.4.10/9.4/3	Ih	U39	K44	60	120	42	30{4}+12{10}
75	Senpintigita granda dekduedro		25/2|5	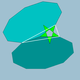10.10.5/2	Ih	U37	K42	60	90	24	12{5/2}+12{10}
76	Rombo-dekdu-dekduedro		5/25|2	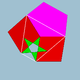4.5/2.4.5	Ih	U38	K43	60	120	54	30{4}+12{5}+12{5/2}
77	Granda kubokubo-okedro		3 4|4/3	8/3.3.8/3.4	Oh	U14	K19	24	48	20	8{3}+6{4}+6{8/3}
78	Kubo-duon-okedro		4/34|3	6.4/3.6.4	Oh	U15	K20	12	24	10	6{4}+4{6}
79	Kubotranĉita kubokedro (Kubo-oktranĉita kubokedro)		4/33 4|	8/3.6.8	Oh	U16	K21	48	72	20	8{6}+6{8}+6{8/3}
80	Du-tritranĉa dekdu-dekduedro		3|5/35	(5/3.5)3	Ih	U41	K46	20	60	24	12{5}+12{5/2}
81	Granda du-tritranĉa dekdu-dudek-dekduedro		3 5|5/3	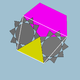10/3.3.10/3.5	Ih	U42	K47	60	120	44	20{3}+12{5}+12{10/3}
82	Malgranda du-tritranĉa dekdu-dudek-dekduedro		5/33|5	10.5/3.10.3	Ih	U43	K48	60	120	44	20{3}+12{5/2}+12{10}
83	Dudek-dekdu-dekduedro		5/35|3	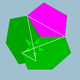6.5/3.6.5	Ih	U44	K49	60	120	44	12{5}+12{5/2}+20{6}
84	Dudektranĉita dekdu-dekduedro		5/33 5|	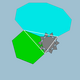10/3.6.10	Ih	U45	K50	120	180	44	20{6}+12{10}+12{10/3}
85	Uniforma granda rombokub-okedro (Kvazaŭrombokubo-okedro)		3/24|2	4.3/2.4.4	Oh	U17	K22	24	48	26	8{3}+(6+12){4}
86	Malgranda rombo-sesedro		3/22 4|	4.8.4/3.8	Oh	U18	K23	24	48	18	12{4}+6{8}
87	Granda du-tritranĉa dudek-dekduedro		3/2|3 5	(5.3.5.3.5.3)/2	Ih	U47	K52	20	60	32	20{3}+12{5}
88	Granda dudek-dudek-dekduedro		3/25|3	6.3/2.6.5	Ih	U48	K53	60	120	52	20{3}+12{5}+20{6}
89	Malgranda dudek-duon-dekduedro		3/23|5	10.3/2.10.3	Ih	U49	K54	30	60	26	20{3}+6{10}
90	Malgranda dekdu-dudekedro		3/23 5|	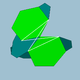10.6.10/9.6/5	Ih	U50	K55	60	120	32	20{6}+12{10}
91	Malgranda dekdu-duon-dekduedro		5/45|5	10.5/4.10.5	Ih	U51	K56	30	60	18	12{5}+6{10}
92	Steligita senpintigita sesedro (Kvazaŭtranĉita sesedro)		2 3|4/3	8/3.8/3.3	Oh	U19	K24	24	36	14	8{3}+6{8/3}
93	Granda senpintigita kubokedro (Kvazaŭtranĉita kubokedro)		4/32 3|	8/3.4.6	Oh	U20	K25	48	72	26	12{4}+8{6}+6{8/3}
94	Granda dudek-dekduedro		2|5/23	(5/2.3)2	Ih	U54	K59	30	60	32	20{3}+12{5/2}
95	Senpintigita granda dudekedro		25/2|3	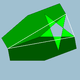6.6.5/2	Ih	U55	K60	60	90	32	12{5/2}+20{6}
96	Rombo-dudekedro		25/23|	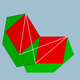6.4.6/5.4/3	Ih	U56	K61	60	120	50	30{4}+20{6}
97	Malgranda steligita senpintigita dekduedro (Kvazaŭtranĉita malgranda steligita dekduedro)		2 5|5/3	10/3.10/3.5	Ih	U58	K63	60	90	24	12{5}+12{10/3}
98	Senpintigita dekduedro (Kvazaŭtranĉita dekduedro)		5/32 5|	10/3.4.10	Ih	U59	K64	120	180	54	30{4}+12{10}+12{10/3}
99	Granda dekdu-dudek-dekduedro		5/23|5/3	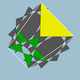10/3.5/2.10/3.3	Ih	U61	K66	60	120	44	20{3}+12{5/2}+12{10/3 }
100	Malgranda dekdu-duon-dudekedro		5/35/2|3	6.5/3.6.5/2	Ih	U62	K67	30	60	22	12{5/2}+10{6}
101	Granda dekdu-dudekedro		5/35/23|	6.10/3.6/5.10/7	Ih	U63	K68	60	120	32	20{6}+12{10/3}
102	Granda dekdu-duon-dudekedro		5/45|3	6.5/4.6.5	Ih	U65	K70	30	60	22	12{5}+10{6}
103	Granda rombo-sesedro		4/33/22|	4.8/3.4/3.8/5	Oh	U21	K26	24	48	18	12{4}+6{8/3}
104	Granda steligita senpintigita dekduedro (Kvazaŭtranĉita granda steligita dekduedro)		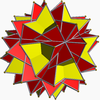2 3|5/3	10/3.10/3.3	Ih	U66	K71	60	90	32	20{3}+12{10/3}
105	Uniforma granda rombo-dudek-dekduedro (Kvazaŭrombo-dudek-dekduedro)		5/33|2	4.5/3.4.3	Ih	U67	K72	60	120	62	20{3}+30{4}+12{5/2}
106	Granda dudek-duon-dekduedro		3 3|5/3	10/3.3/2.10/3.3	Ih	U71	K76	30	60	26	20{3}+6{10/3}
107	Granda dekdu-duon-dekduedro		5/35/2|5/3	10/3.5/3.10/3.5/2	Ih	U70	K75	30	60	18	12{5/2}+6{10/3}
108	Granda senpintigita dudek-dekduedro (Granda kvazaŭtranĉita dudek-dekduedro)		5/32 3|	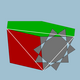10/3.4.6	Ih	U68	K73	120	180	62	30{4}+20{6}+12{10/3}
109	Granda rombo-dekduedro		3/25/32|	4.10/3.4/3.10/7	Ih	U73	K78	60	120	42	30{4}+12{10/3}
110	Malgranda riproĉa dudek-dudek-dekduedro		|5/23 3	3.3.3.3.3.5/2	Ih	U32	K37	60	180	112	(40+60){3}+12{5/2}
111	Riproĉa dekduedro		|25/25	3.3.5/2.3.5	I	U40	K45	60	150	84	60{3}+12{5}+12{5/2}
112	Riproĉa dudek-dekdu-dekduedro		|5/33 5	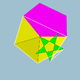3.3.3.3.5.5/3	I	U46	K51	60	180	104	(20+6){3}+12{5}+12{5/2}
113	Granda inversigita riproĉa dudek-dekduedro		|5/32 3	3.3.3.3.5/3	I	U69	K74	60	150	92	(20+60){3}+12{5/2}
114	Inversigita riproĉa dekdu-dekduedro		|5/32 5	3.5/3.3.3.5	I	U60	K65	60	150	84	60{3}+12{5}+12{5/2}
115	Granda riproĉa dekdu-dudek-dekduedro		|5/35/23	3.5/3.3.5/2.3.3	I	U64	K69	60	180	104	(20+60){3}+(12+12){5/2}
116	Granda riproĉa dudek-dekduedro		|25/25/2	3.3.3.3.5/2	I	U57	K62	60	150	92	(20+60){3}+12{5/2}
117	Granda malantaŭe riproĉa dudek-dekduedro		|3/25/32	(3.3.3.3.5/3)/2	I	U74	K79	60	150	92	(20+60){3}+12{5/2}
118	Malgranda malantaŭe riproĉa dudek-dudek-dekduedro		|3/23/25/2	(3.3.3.3.3.5/2)/2	Ih	U72	K77	180	60	112	(40+60){3}+12{5/2}
119	Granda durombo-dudek-dekduedro		|3/25/335/2	(4.5/3.4.3.4.5/2.4.3/2)/2	Ih	U75	K80	60	240	124	40{3}+60{4}+24{5/2}

Eksteraj ligiloj |

• Magnus J. Wenninger


• Programaro uzita por generi bildojn en ĉi tiu artikolo:
  
  
  
  • 
    Stella: Pluredra Navigilo - programaro Stella, uzita por generi la kolorigitajn modeloj sur ĉi tiu paĝo. Ĝi povas krei kaj printi retojn por ĉiuj pluredraj modeloj de Wenninger.
  
  
  • 
    Pluredra Steliga Apleto de Vladimir Bulatov (Uzita por generi la steligajn bildojn sur ĉi tiu paĝo)
  
  
  
  


• Galerio de pluredraj Modeloj