Gfyuki

	; Okedro;
Plia nomo;	; Triangula kontraŭprismo;
	; ;
	; ;
	; Klaku por rigardi turnantan bildon;
; Speco;	; Regula pluredro ; Trianguledra pluredro;
; Vertica figuro;	3.3.3.3;
; Bildo de vertico;	; ;
; Bildo de reto;	; ;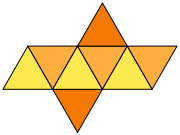
; Simbolo de Wythoff;	4 \| 2 3;
; Simbolo de Schläfli;	{3,4} ; kaj {33}{displaystyle {begin{Bmatrix}3\3end{Bmatrix}}};
; Figuro de Coxeter-Dynkin;	; ;
; Indeksoj;	U05 C17W2;
; Simbolo de Bowers;	Oct;
; Verticoj;	6;
; Lateroj;	12;
; Edroj;	8;
; Edroj detale;	8{3};
; χ;	2;
; Geometria simetria grupo;	; Oh;
; Duedra angulo;	arccos(-1/3) ~= 109,47122°;
; Duala;	; Kubo;
; Bildo de duala;	; ;
; ; v • d • r; ;	; ;

Okedro estas pluredro kun 8 edroj. La regula okedro estas platona solido komponita el de 8 egallateraj trianguloj. En ĉiu vertico kuniĝas 4 edroj.

La okedra geometria simetria grupo estas O_h de ordo 48. Subgrupoj de ĉi tiu grupo estas D_3d (ordo 12), la geometria simetria grupo de triangula kontraŭprismo; D_4h (ordo 16), la geometria simetria grupo de kvadrata dupiramido; T_d (ordo 24), la geometria simetria grupo de rektigita kvaredro. Ĉi tiuj simetrioj povas esti emfazitaj per malsamaj dekoracioj de la edroj.

Ĝi estas tri-dimensia kruca hiperpluredro. Ĝi estas ankaŭ triangula kontraŭprismo.

La regula okedro havas 6 verticojn kaj 12 randojn, ĉi tio estas la minimumo inter diversaj okedro; neregulaj okedroj povas havi 12 verticojn kaj 18 randojn. ^[1]

Estas kvar grava specoj de okedroj kun duedra simetrio:

Seslatera prismo: 6 kvadratoj, 2 seslateroj

Seplatera piramido: 7 trianguloj, 1 seplatero

Kvarlatera dupiramido: 8 trianguloj, kutime izocelaj, en ĉi tiun specon trafas la regula okedro se la trianguloj estas egallateraj.

Kvarlatera trapezoedro - 8 deltoidoj

La vorto okedro estas malofte uzata en ĉi tiu ĝenerala senco ĉar ĉi tiuj pluredroj ne havas gravajn komunajn propraĵoj.

Enhavo

1 Karteziaj koordinatoj

2 Areo kaj volumeno

3 Geometriaj rilatoj

4 Rilatantaj pluredroj

5 Uzo

6 Diversaĵoj

7 Vidu ankaŭ

8 Referencoj

9 Eksteraj ligiloj

Karteziaj koordinatoj |

Karteziaj koordinatoj de verticoj de dudekedro centrita je la nulo de koordinatoj kun longo de lateroj 3^1/2:

( ±1, 0, 0 );

( 0, ±1, 0 );

( 0, 0, ±1 ).

Areo kaj volumeno |

La areo A kaj la volumeno V de regula okedro de randa longo a estas:

{displaystyle A=2{sqrt {3}}a^{2}approx 3.46410162a^{2}}

{displaystyle V={frac {1}{3}}{sqrt {2}}a^{3}approx 0.471404521a^{3}}

Tial la volumeno estas kvaroble pli granda de tiu de regula kvaredro kun la sama randa longo, kaj la surfaca areo estas duoble pli granda (ĉar estas 8 sed ne 4 trianguloj).

Geometriaj rilatoj |

La eno de la kombinaĵo de du duale lokigitaj kvaredroj estas okedro, kaj ilia kombinaĵo stelokangulopluredro, estas la sola steligo de okedro.

Okedroj kaj kvaredroj povas esti alterne uzataj por formi vertico-uniforman, latero-uniforman kaj edro-uniforman kahelaro de spaco.Ĝi estas unu el la 28 konveksaj uniformaj ĉelaroj. Ankaŭ estas kahelaro el okedroj kaj kubokedroj.

Rilatantaj pluredroj |

La okedro povas ankaŭ esti konsiderata kiel rektigita kvaredro.

Vico inter kvaredro kaj ĝia dualo:

Kvaredro

Senpintigita kvaredro

Okedro

Senpintigita kvaredro

Kvaredro

Uzo |

Natura kristaloj de diamanto aŭ aluno estas kutime okedraj.

La regula dekduedro estas ofte uzita en rolludoj kiel 8-flankita ĵetpluredro ("d8" mallonge).

Diversaĵoj |

Se ĉiu rando de okedro estas anstataŭigita per 1 omaj rezistancilo, la rezistanco inter kontraŭaj verticoj estas 1/2 omoj kaj tiu inter najbaraj verticoj estas 5/12 omoj.^[2]

Vidu ankaŭ |

Trilateropiramidigita okedro

Piramidigita dekduedro

Senpintigita okedro

Okedra molekula geometrio

Uniformaj pluredraj kombinaĵoj de okedroj
- Kombinaĵo de 4 okedroj kun turna libereco
- Kombinaĵo de 8 okedroj kun turna libereco
- Kombinaĵo de 4 okedroj
- Kombinaĵo de 20 okedroj kun turna libereco
- Kombinaĵo de 20 okedroj
- Kombinaĵo de 10 okedroj
- Kombinaĵo de 5 okedroj

Kombinaĵo de kubo kaj okedro

Triangulaj geometriaj figuroj
Triangula piramido \| Triangula prismo \| Triangula kontraŭprismo \| Triangula trunko \| Triangula kajtopluredro \| Triangula senpintigita kajtopluredro \| Triangula dupiramido \| Triangula dutrunko \| Triangula plilongigita dupiramido \| Triangula kupolo \| Triangula ortodukupolo \| Triangula turnodukupolo

Pluredroj laŭ kvanto de edroj
Duedro \| Triedro \| Kvaredro \| Kvinedro \| Sesedro \| Sepedro \| Okedro \| Naŭedro \| Dekedro \| Dekduedro \| Dudekedro \| Dudekkvaredro
Noto ke en la listo pli supre estas ne ĉiuj eblaj kvantoj da edroj.

Referencoj |

↑ [1]

↑ Duglaso J. Klein (2002). “Resistance-Distance Sum Rules - Rezisto-distancaj sumaj reguloj”, Croatica Chemica Acta (PDF) 75 (2), p. 633–649. Alirita 2006-09-30..

Eksteraj ligiloj |

Okedro

La uniformaj pluredroj

Virtualaj realaj pluredroj

Paperaj modeloj de pluredroj

[1] [1]

[2] Duglaso J. Klein (2002). “Resistance-Distance Sum Rules - Rezisto-distancaj sumaj reguloj”, Croatica Chemica Acta (PDF) 75 (2), p. 633–649. Alirita 2006-09-30..

搜尋此網誌

Gfyuki

Okedro