Gfyuki

Parto de serio pri
Scienco
Formalaj sciencoj Logiko Matematiko Matematika logiko Matematika statistiko Teoria komputila scienco
Fizikaj sciencoj Fiziko Klasika fiziko Moderna fiziko Aplikata fiziko Eksperimenta fiziko Teoria fiziko Komputada fiziko Termodinamiko Meĥaniko Solida meĥaniko Klasika meĥaniko Kontinuaĵa mekaniko Reologio Mekaniko de fluidaĵo Plasmo Atoma fiziko Fiziko de kondensita materio Kvantuma meĥaniko Nuklea fiziko Partikla fiziko Speciala relativeco Kvantuma kampa teorio Ĝenerala relativeco Kordoteorio Ĥemio Redoksa reakcio Alkemio Analiza kemio Astrokemio Biokemio Kristalografio Media kemio Manĝaĵokemio Geokemio Verda kemio Neorganika kemio Materiala inĝenierarto Molekula fiziko Nuklea kemio Organika kemio Fotokemio Fizika kemio Radiokemio Solidstata kemio Stereokemio Supermolekula kemio Surfacoscienco Teoria kemio Astronomio Astrofiziko Kosmologio Galaksiastronomio Planeda geologio Planedoscienco Stela astronomio Tersciencoj Meteorologio Klimatologio Ekologio Media scienco Geodezio Geologio Geomorfologio Geofiziko Glaciologio Hidrologio Limnologio Oceanografio Paleoklimatologio Paleoekologio Polenoscienco Pedologio Edafologio Fizika geografio Spaca scienco
Vivosciencoj Biologio Anatomio Astrobiologio Bioĥemio Biogeografio Biologia inĝenierarto Biofiziko Konduta neŭroscienco Biotekniko Botaniko Ĉelbiologio Konservobiologio Kriobiologio Disvolviĝ-biologio Ekologio Etnobiologio Etologio Evolubiologio) Genetiko (Enkonduko al genetiko) Gerontologio Imunologio Limnologio Marbiologio Mikrobiologio Molekula biologio Neŭroscienco Paleontologio Parazitologio Fiziologio Radiobiologio Edafo Sociobiologio Sistematiko Toksologio Zoologio
Sociaj sciencoj Antropologio Arkeologio Kriminologio Demografio Ekonomiko Edukado Internaciaj rilatoj Juro Lingvistiko Politika scienco Psikologio Sociologio Soci-ekonomia geografio
Aplikataj sciencoj Inĝenierarto Aerospaca scienco Agrikultura Biomedicina Kemia inĝenierarto Civila inĝenierarto Komputila scienco Komputika inĝenierarto Elektra inĝenierarto Fajroprotekto Genteĥniko Industria inĝenierarto Meĥanika inĝenierarto Milita inĝenierarto Mineja inĝenierarto Nuklea inĝenierarto Operacia esploro Programada inĝenierarto Robotiko TTT-inĝenierarto Sansciencos Biologia inĝenierarto Dentokuracado Epidemiologio Sankuracado Medicino Flegado Farmacio Socia laboro Veterinara medicino
Interdisciplineco Aplikata fiziko Artefarita inteligenteco Bioetiko Biokomputiko Biomedika inĝenierarto Biostatistiko Kognoscienco Kompleksaj sistemoj Komputada lingvoscienco Kulturaj sciencoj Kibernetiko Mediscienco Media socia scienco Mediaj studoj Etnaj studoj Evolua psikologio Forstado Sano Bibliotekscienco Matematika kaj teoria biologio Matematika fiziko Militistiko Retscienco Neurona inĝenierarto Neŭroscienco Sciencaj studoj Scienco, teĥnologio kaj socio Scienca modelado Semiotiko Sociobiologio Statistiko Sistemscienco Transdisciplino Urba planado TTT-sciencoj
Filozofio kaj historio de scienco Civitanoscienco Marĝenscienco Historio de scienco Filozofio de scienco Protoscienco Pseŭdoscienco Scienca libereco Scienca politiko Scienca metodo Teĥnoscienco
Ĝeneralaĵoj Portalo Kategorio
v • d • r

Statistiko estas scienco pri la metodoj kolekti, analizi kaj interpreti empiriajn nombrajn donitaĵojn kaj kiel prezenti la rezulton. Tio fariĝas komplike, kiam la donitaĵoj kaj la interdependoj ne estas tute konataj, estas neprecizaj aŭ tro multenombraj por esti detale traktataj. Statistiko estas rimedo kompari sciencan teorion kun la reala mondo
kaj serĉo de novaj interrilatoj por nova teorio.

Statistiko uzas probablon, matematikan mezurteorion kaj modeligon.
Nuntempe matematiko, komputiko kaj statistiko formas novan kampon, donitaĵanalizon, kun novaj rimedoj por kalkulado, modeligo, inferenco kaj prezento.

Kvanteca scienca esplorado baziĝas sur statistikaj metodoj (kp. kvaliteca esplorado).

Oni uzas la nomon statistiko (minuskle kaj ofte plurale) ankaŭ por la datumoj mem aŭ la tabelo ellaborita laŭ la metodoj de la Statistiko.

Teorio de Statistiko |

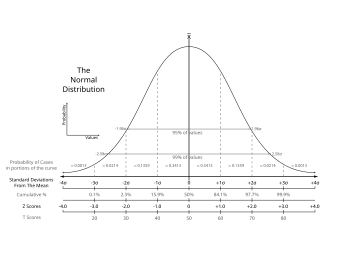
Normala distribuo.

Statistiko estas transversa apogo al ampleksa varieco de disciplinoj, de la fiziko ĝis la sociaj sciencoj, de la sciencoj de la sano ĝis la kontrolo de kvalito. Ĝi estas uzata por la decidado en areoj de negocoj aŭ institucioj registaraj.

La statistiko dividiĝas en du grandaj areoj:

• La priskriba statistiko, kiu dediĉas sin al la metodoj de rekolektado, priskribo, elmontrado kaj resumo de datumoj estigitaj de la fenomenoj studataj. La datumoj povas esti resumitaj nombre aŭ grafike. Bazaj Ekzemploj de parametroj statistikaj estas: la aritmetika meznombro kaj la varianca devio.


• La dedukta statistiko, kiu dediĉas sin al la generado de la modeloj, deduktoj kaj antaŭdiroj asociitaj al la fenomenoj studataj konsiderante la hazardecon de la observoj. Oni ĝin uzas por modeli regulojn en la datumoj kaj ĉerpi konkludojn. Ĉi tiuj deduktaĵoj povas preni la formon de respondoj al demandoj se/ne (provo de hipotezo), alpreno de nombraj karakterizaĵoj, prognozoj de futuraj observoj, priskriboj de asocio (korelacio) aŭ modelado de rilatoj inter variabloj. Aliaj teknikoj de modelado estas anova, serioj de tempo kaj minado de datumoj.

Ambaŭ branĉoj apartenas al la Aplikita Statistiko. Estas ankaŭ disciplino nomata Matematika Statistiko, kiu referencas al la teoriaj bazoj de la materio. La vorto «statistikoj» ankaŭ aludas al la rezulto apliki algoritmon statistikan al aro de datumoj, kiel en statistikoj ekonomiaj, statistikoj kriminalaj, inter aliaj.

Etimologio |

La germana termino Statistik, kiu estis unue enkondukita de Gottfried Achenwall (1749), referencis origine al la analizo de datumoj de la Ŝtato, tio estas, la "scienco de la ŝtato" (ankaŭ nomita aritmetika politiko laŭ ĝia rekta tradukado). Ne estis ĝis la 19a jarcento kiam la termino statistiko akiris la signifon de kolektado kaj klasifikado de datumoj. Ĉi tiu koncepto estis enkondukita de la anglo John Sinclair.

Originoj en probablo |

Christiaan Huygens donis la unuan sciencan traktadon de la fako

La metodoj statistika-matematikaj emerĝis de la teorio de probablo, kiu datiĝas de la mesaĝado inter Blaise Pascal kaj Pierre de Fermat (1654). Christiaan Huygens (1657) donis la unuan sciencan traktadon de la fako. La Ars coniectandi (postmorta, 1713) de Jakob Bernoulli kaj la Doktrino de ebloj (1718) de Abraham de Moivre studis la disciplinon kiel branĉo de la matematikoj. En la moderna erao, la laboro de Andrej Kolmogorov estis kolono en la formulado de la fundamenta modelo de la Teorio de Probableco, kiu estas uzita tra la statistiko.

Pierre-Simon Laplace (1774) faras la unuan provon dedukti regulon por la ĉifro de observoj de la komencoj de la teorio de probabloj. Laplace reprezentis la leĝon de probabloj de eraroj per kurbo kaj li deduktis formulon por la mezumo de tri observoj.
La metodo de kvadrataj minimumoj, kiu estis uzita por minimumigi la erarojn en mezuradoj, estis eldonita sendepende por Adrien-Marie Legendre (1805), Robert Adrain (1808), kaj Carl Friedrich Gauss (1809). Gaŭso estis uzinta la metodon en lia fama antaŭdiro de la lokigado de la nanoplanedo Cereso en 1801. Pliaj provoj estis skribitaj de Laplace (1810, 1812), Gaŭso (1823), James Ivory (1825, 1826), Hagen (1837), Friedrich Bessel (1838), W.F. Donkin (1844, 1856), John Herschel (1850) kaj Morgan Crofton (1870). Aliaj kontribuintoj estis Ellis (1844), Augustus De Morgan (1864), Glaisher (1872) kaj Giovanni Schiaparelli (1875). La formulo de Peters por r{displaystyle r}, la probabla eraro de simpla observo estas bone konita.

La 19a jarcento inkludas aŭtorojn kiel Laplace, Silvestre Lacroix (1816), Littrow (1833), Richard Dedekind (1860), Helmert (1872), Hermann Laurent (1873), Liagre, Didion kaj Karl Pearson. Augustus De Morgan kaj George Boole plibonigis la prezenton de la teorio. Adolphe Quetelet (1796-1874),fariĝis alia grava fondinto de la statistiko kaj enkondukis la nocion de la «averaĝa homo» (l’homme moyen) kiel maniero kompreni la kompleksajn sociajn fenomenojn.

Aktuala stato |

La modelo IS-LM estas uzata por analizi la efikon de peteksplodo en ekonomiko (cikla sendungeco).

Dum la 20a jarcento, la kreo de precizaj instrumentoj por aferoj de publika sano (Epidemiologio, biostatistiko, ktp.) kaj sociaj kaj ekonomiaj celoj (proporcio de senlaboreco, Ekonometrio, ktp.) necesigis la konstantan uzadon de la oportunaj statistikoj.

Hodiaŭ la uzo de la statistiko etendiĝis for de ĝiaj originoj kiel servo al la Ŝtato aŭ al la registaro. Personoj kaj organizoj uzas statistikon por kompreni datumojn kaj preni decidojn en sociaj kaj naturaj sciencoj, medicino, negocoj kaj aliaj areoj. La statistiko estas komprenita ĝenerale ne kiel sub-areo de la matematikoj sed kiel malsama scienco «aliancita». Multaj universitatoj havas akademiajn fakojn de matematiko kaj statistiko aparte. La statistiko instruas en fakoj tiel diversaj kiel psikologio, eduko kaj publika sano.

Bazaj konceptoj kaj rezultoj donitaj de Teorio de probabloj |

Se la probablodistribuo de variablo X estas normala, la
aritmetika averaĝo estas la plej efika (minimumvarianca)
pritakso de ekspekto de la variablo:

E^=X¯=1n⋅∑i=1nxi{displaystyle {hat {E}}={bar {X}}={frac {1}{n}}cdot sum _{i=1}^{n}x_{i}}

kaj la ekspektofidela estimanto por la varianco σ2{displaystyle {sigma }^{2}} estas

σ^2=1n−1⋅∑i=1n(xi−X¯)2{displaystyle {hat {sigma }}^{2}={frac {1}{n-1}}cdot sum _{i=1}^{n}(x_{i}-{bar {X}})^{2}}

La kvadratradiko σ^{displaystyle {hat {sigma }}} pritaksas disiĝgradon de la xi{displaystyle x_{i}}
(kvankam ne estas ekspektofidela pritakso de σ{displaystyle {sigma }}).

Praktike oni plej ofte uzas la suprajn pritaksojn, kiam oni volas scii
lokon ĉirkaŭ kiu X varias kaj la koncernan gradon de disiĝo.

Statistikaj metodoj |

Oni povas dividi statistikajn metodojn diversmaniere:

1. laŭ la nombro de traktataj variabloj: ĉu unu, du aŭ pli


2. kiom oni scias pri valoroj de variablo: ĉu oni scias ilin perfekte,

t.e. la distribuo estas konata (parametra metodo), aŭ en alia ekstremo,
la valoroj estas kodigitaj per klaso aŭ vicnombro (neparametra metodo)

Grafikaĵo de sonorila kurbo pri normala distribuo.

Histogramo de nombroj de okazaĵoj laŭ iliaj valoroj, la plej oftaj valoroj estas ĉircaŭ 100.

Famaj statistikistoj |

Andrej Nikolajeviĉ Kolmogorov

Ĉefa sidejo de la Nacia Instituto de Statistiko, en Madrido (Hispanio), konstruita en 1973 kaj rehabilitigita en 2008.

• Pafnutij Ĉebiŝov


• René Descartes


• Milton Friedman


• Carl Friedrich Gauss


• Andrej Kolmogorov


• Isaac Newton


• Florence Nightingale


• Blaise Pascal


• Adolphe Quételet

Vidu ankaŭ |

Bibliografio |

• Best, Joel (2001). Damned Lies and Statistics: Untangling Numbers from the Media, Politicians, and Activists. University of California Press. ISBN 0-520-21978-3.


• Hacking, Ian (1990). The Taming of Chance. Cambridge University Press. ISBN 0-521-38884-8.


• Lindley, D. V. (1985). Making Decisions (2.ª edición edición). John Wiley & Sons. ISBN 0-471-90808-8.


• Stigler, Stephen M. (1990). The History of Statistics: The Measurement of Uncertainty before 1900. Belknap Press/Harvard University Press. ISBN 0-674-40341-X.


• Tijms, Henk (2004). Understanding Probability: Chance Rules in Everyday life. Cambridge University Press. ISBN 0-521-83329-9.


• Volle, Michel (1984). Le métier de statisticien (2a eld.). Económica. ISBN 2-7178-0824-8. rete


• Bernard Delmas, Statistique descriptive pour l’économie et la gestion, Presses Universitaires du Septentrion, 2009 (ISBN 978-2-7574-0074-6).


• Jean-Pierre Favre, Mathématiques de gestion, Digilex, 2009 (ISBN 978-2-940404-01-8).


• Olivier Martin, L'enquête et ses méthodes : l'analyse de données quantitatives, Paris, Armand Colin, 2005 puis 2009.


• Michel Volle, Histoire de la statistique industrielle, Economica, 1982, ISBN 2-7178-0520-6, rete.


• Georges Hostelet, Le concours de l’analyse mathématique à l’analyse expérimentale des faits statistiques, Paris, Hermann, Actualités Scientifiques et Industrielles, no 585), 1937, 70 pp.


• T.H. kaj R.J. Wonnacott, Statistique, éd. Economica, 1995 (4e éd.), 922 p., ISBN 2-7178-2072-8
  


• Gilbert Saporta, Probabilités, Analyse des données et Statistiques, Paris, Éditions Technip,‎ 2006, 622 p. (ISBN 978-2-7108-0814-5, rete)


• Mathieu Rouaud, Probabilités, statistiques et analyses multicritères Un livre de 182 pages pour s'initier à la statistique.


• Nicolas Gauvrit, Statistiques : Méfiez-vous !, Ed. Ellipses (Paris), 2007, ISBN 978-2-7298-3070-0
  


• Stéphanie Dupays, "Déchiffrer les statistiques économiques et sociales" Ed. Dunod, 2008, ISBN 2-10-051584-5
  


• Alain Desrosières, La politique des grands nombres : histoire de la raison statistique, Paris, La Découverte,‎ 2000 (ISBN 978-2-7071-6504-6) (2004). La política de los grandes números. Ed. Melusina. ISBN 84-933273-5-2.


• Anders Hald, A History of Mathematical Statistics, New-York, Wiley,‎ 1998 (ISBN 0-471-17912-4)


• David Salsburg, The Lady Tasting Tea : How statistics revolutionized science in the twentieth century, Holt McDougal,‎ mai 2002, 1e éd. (ISBN 978-0-8050-7134-4)

Eksteraj ligiloj |

• Enkonduko al la Deskripta Statistiko


• Enkonduko al la Konkluda Statistiko